Por Rafael Alemañ
Resumen. El anuncio en julio de 2012 de los primeros indicios experimentales sobre la existencia del bosón de Higgs, reavivó el interés de la secular debate sobre el significado de conceptos como el vacío, los campos físicos o incluso la propia noción de espacio. La evolución de sus interpretaciones revela mutaciones profundas en nuestra visión de la naturaleza. En este artículo se pretende exponer la complejidad del concepto de vacío, clásico y cuántico, así como su relación con otras propiedades del espacio-tiempo, como la gravitación. Consecuencia de todo ello es que el moderno concepto de vacío físico encierra una enorme riqueza conceptual todavía por explorar.
1.1 Introducción
La mayoría de nosotros, en los momentos de crisis, solemos identificar el vacío con el estado de nuestros bolsillos o con nuestras perspectivas de futuro. El vacío, la ausencia de cualquier cosa concebible, parece ser el estado físico más simple de abordar por el mero hecho de que su propia definición implica que nada hay en él que describir. Y esa idea resulta ajustada a la realidad –y no del todo– dentro del marco que nos proporcionaba la física clásica.
Pero cuando la teoría cuántica entró en escena a principios del siglo XX, las sacudidas provocadas en el conjunto de nuestro conocimiento del mundo físico no dejaron indiferente ni siquiera al apacible vacío. Desde entonces lo que aparentaba no contener cosa alguna se convirtió en un bullicioso mar de partículas virtuales, apareciendo y despareciendo como por ensalmo. O esa es, al menos, la imagen que nos transmite la mayoría de los manuales de divulgación científica cuando se atreven a abordar este tema, algo no demasiado frecuente.
Buena parte de razón no les falta, porque se trata de una imagen muy impactante y bastante cercana a la realidad. Sin embargo, son también muchas las imprecisiones que se suelen mezclar con las exposiciones al uso de las propiedades cuánticas del vacío. El motivo de tales confusiones, sin duda, estriba en que el vacío cuántico es un estado físico peculiar, lleno de sutilezas y complejidades que ni siquiera los expertos dominan por completo. Debemos, pues, mostrar indulgencia con los errores ajenos si esperamos tenerla con los nuestros. Aun así, merecerá la pena sumergirnos en el fascinante descenso a las entrañas del vacío cuántico, donde nos esperan fenómenos asombrosos y enigmas inquietantes.
1.2 Primeros pasos en el vacío
Aristóteles rechazó la existencia en el mundo real del vacío absoluto –la completa ausencia de cualquier cosa– razonando por reducción al absurdo sobre la base de su propia concepción del movimiento físico. Para el filósofo griego una mera observación de los hechos cotidianos probaba que la velocidad de los cuerpos impulsados por una fuerza determinada, dependía de la resistencia del medio en el que se desplazasen. Un individuo que corriese con el agua hasta la cintura, digamos, encontraría más resistencia a su avance que quien lo hiciese en el aire, y éste último se movería lógicamente con mayor velocidad. Aristóteles dedujo así que un objeto sobre el que actúa una fuerza cualquiera, de hallarse en el vacio absoluto, no encontraría oposición alguna a su avance y alcanzaría una velocidad infinita. Los filósofos griegos se llevaban mal con el infinito, de modo que esta conclusión le pareció a Aristóteles una buena excusa para proscribir la existencia del vacío.
De esta convicción nació la idea del “horror al vacío” (el horror vacuum de los clásicos) que de forma tan natural explicaba numerosas observaciones de la vida diaria. El efecto de los sifones neumáticos era una de ellas; tomemos un tubo de goma no muy largo, y cerrando uno de sus extremos aspiremos con fuerza por el otro mientras lo sumergimos en un líquido. Si en el mismo instante de la inmersión abrimos el extremo cerrado y dejamos de aspirar por el otro, comprobaremos que un flujo de líquido comenzará a salir por el orificio abierto. La explicación aristotélica era obvia: al aspirar hemos creado un vacío –imperfecto, pero vacío al fin y al cabo– dentro del tubo, circunstancia que la naturaleza trata de compensar llenándolo con el líquido lanzado a su través.
El debate sobre el vacío se prolongó hasta el siglo XVII, cuando dos titanes intelectuales como Descartes y Newton tomaron partido por cada una de las opiniones en liza. El francés René Descartes (1596 – 1650), que en esto podría ser considerado el último de los autores aristotélicos notables, no creía en el vacío en modo alguno (Gaukroger 2002). A su juicio, desde los espacios entre cuerpos celestes hasta los huecos entre las partes más pequeñas de cualquier objeto, se hallaban permeados por un fluido sutil que –también en la tradición griega– llamaba “éter” (Lorentz 1927). Los vórtices y remolinos en el éter explicaban, por ejemplo, el movimiento incesante de los astros.

Por el contrario, el inglés Isaac Newton (1643 – 1727) sí admitía la posibilidad de un vacío perfecto, en el cual se moviesen los cuerpos físicos bajo la acción de las fuerzas contempladas en sus leyes del movimiento. No había en la mecánica de Newton impedimento alguno para que un objeto sometido a una fuerza constante acelerase hasta una velocidad infinita, aunque para ello necesitase también un tiempo infinito; el límite de la velocidad de la luz aún quedaba lejos en el horizonte histórico.
Pese a ello, el genio británico fracasó en la búsqueda de un proceso físico que explicase la propagación de la fuerza gravitatoria entre cuerpos, como los celestes, sin contacto mutuo. Las bolas de billar entrechocando sobre un tablero constituían un magnífico ejemplo de sus otras leyes dinámicas, pero nada había que explicase la atracción de la gravedad a distancia a través del espacio vacío entre estrellas y planetas. Así que finalmente incluso Newton hubo de admitir la hipotética presencia de un éter cuyas vibraciones serían las responsables de producir las atracciones expresadas en su ley de la gravitación universal.
La noción del éter como un fluido omnipresente que llenaba el universo hasta sus más íntimos intersticios, sobrevivió hasta principios del siglo XX, debido a que se consideraba la única explicación plausible para justificar la transmisión de ondas electromagnéticas a través del vacío sideral. En la física clásica toda onda se entendía como una oscilación en un medio elástico preexistente, ya fuesen olas en el agua o vibraciones en el aire como las del sonido. La luz era una onda electromagnética, y por tanto parecía obligado a buscar un medio que actuase como soporte material de sus vibraciones. Para explicar que la luz emitida por el Sol llegase hasta la Tierra, el éter se suponía el mejor candidato disponible; de hecho el único. La relatividad de Einstein lo despojó de su única función, aceptando que las ondas electromagnéticas pueden propagarse en el vacío a diferencia de las ondas elásticas usuales, y el éter se sumió lentamente en el olvido.

Los avances tecnológicos del siglo XVIII demostraron que el supuesto “horror al vacío” no era tal, sino la manifestación de una propiedad física previamente ignorada, la presión atmosférica (De Segovia 2010). En efecto, el aire, como cualquier sistema material, se ve atraído gravitatoriamente por nuestro planeta, y es el peso de la columna de aire que descansa sobre un determinado punto de la superficie terrestre lo que denominamos presión atmosférica en ese punto. Más que en el horror de la naturaleza al vacío creado dentro del tubo, la causa del efecto sifón antes mencionado había de buscarse en la diferencia de presiones que producía la succión entre ambos extremos. La bomba de vacío puesta a punto durante el Siglo de las Luces, así como los experimentos de Torricelli para estimar la presión atmosférica (empleando columnas de vidrio llenas de mercurio), allanaron el camino para admitir que, después de todo, el vacío sí era un estado físicamente asequible.
1.3 El vacío clásico, no tan vacío
Una de las formas más cómodas de estimar el grado de vacío en el interior de una vasija cerrada, consistía en aplicarle cuidadosamente un manómetro para tener una lectura directa de la presión en su interior. A mayor vacío, menor presión; pocas dudas había al respecto. Y en el caso límite, se tendría una presión cero al llegar a un vacío absoluto. Se reconocía que quizás no había bombas de succión tan poderosas como para llegar a ese resultado, pero también se afirmaba que semejante dificultad era tan solo de carácter técnico, no teórico. No parecía haber un impedimento de principio que impidiese obtener un vacío perfecto. ¿O sí lo había? Pues en realidad sí, ya que aún faltaba por entrar en escena un protagonista indispensable en este drama.
El siglo XIX saludó la consolidación de una nueva rama de la ciencia física dedicada al estudio de los intercambios energéticos, la temodinámica, que tan relevante papel jugaría en la trepidante Revolución Industrial entonces en curso. De sus avances aplicados a los primeros modelos atómicos de la materia, se dedujo que la temperatura representaba la energía media de vibración de los átomos o las moléculas de un objeto. Una escala de temperaturas basada en esta interpretación, asignaría el valor cero al estado en que tales componentes microscópicos carecen de todo movimiento. Si los átomos de un material se encuentran en reposo, tanto su energía de vibración como la temperatura a ella asociada se anularán. Semejante escala térmica recibió el nombre de "escala absoluta de temperaturas", o también "escala Kelvin" en honor a William Thomson (1824 - 1907), Lord Kelvin, el científico británico que la ideó. Ahora bien, investigaciones realizadas por James Dewar (1842 – 1923), Walther Nernst (1864 – 1941) y Max Planck (1858 – 1947) determinaron la imposibilidad de enfriar cualquier sistema físico hasta el cero absoluto en un número finito de etapas sucesivas. El que más tarde sería conocido como el Tercer Principio de la Termodinámica, relegaba el cero absoluto a la condición de estado ideal inalcanzable en la práctica.
Tal vez no lo pareciese, pero tales cuestiones revestían gran importancia para la discusión sobre la posibilidad física de lograr un vacío perfecto. La teoría electromagnética −cuyos progresos también marcaron el siglo XIX− afirmaba que cualquier cuerpo por encima del cero absoluto emitiría algún tipo de radiación. Por tanto, aunque tomásemos un recipiente y lo vaciásemos por completo de todo su contenido mediante potentísimas bombas de succión, todavía nos quedarían las radiaciones electromagnéticas que penetrasen desde el exterior. Y si consiguiésemos aislarlo de las radiaciones externas, no podemos olvidar que las paredes del contenedor, dado que no podrían enfriarse hasta el cero absoluto, emitirían una cierta radiación que llenaría ese espacio interior supuestamente vacío.

El problema no era desdeñable, por cuanto el escocés James Clerk Maxwell (1831 – 1879), uno de los fundadores del electromagnetismo, hablaba en su magna obra Tratado sobre la Electricidad y el Magnetismo (1873), de la presión ejercida sobre una superficie por la radiación electromagnética. Y no cabe duda de la inconveniencia de considerar vacío un recipiente en cuyo interior existe un ente físico, la radiación electromagnética, capaz de ejercer presión sobre sus paredes.
Con todo, los físicos no se desanimaron. Era verdad que ahora sí existía un obstáculo fundamental que imposibilitaba enfriar un sistema hasta el cero absoluto, y que contando con la radiación ambiental ningún recipiente estaría completamente vacío. Pero también resultaba cierto que las leyes naturales permitían una aproximación arbitrariamente cercana a ese vacío ideal. Aunque jamás lo alcanzásemos, el vacío estaría cada vez más y más cerca de nosotros. O eso se suponía hasta la irrupción en el escenario de la teoría cuántica.
1.4 Osciladores cuánticos
En el plano científico, el siglo XX se recordará por haber acogido dos de las grandes revulsiones intelectuales de la historia humana: la relatividad y la física cuántica. La primera nos enseñó la esencial equivalencia entre masa y energía, la inextricable conexión entre el espacio y el tiempo, así como la interpretación de la gravedad en términos de la curvatura espacio-temporal. A la segunda debemos que el pulcro y gentil mundo macroscópico, gobernado por leyes deterministas, se disolviese a nivel microscópico en un bullicio fantasmal de partículas carentes de atributos tan esenciales para nuestra comprensión como la forma, la posición o la velocidad.
Era inevitable que estas dos grandes realizaciones científicas dejaran pronto su huella sobre el problema del vacío. En la fase que se dio en llamar "primera cuantización", los investigadores se ocuparon de explorar las nuevas propiedades cuánticas de las partículas materiales conocidas entonces (átomos, protones, electrones,...), mientras se dejaba para un segundo paso, denominado "segunda cuantización", la búsqueda de una descripción cuántica que abarcase tanto la materia como los campos de fuerzas (Aitchison 1985).
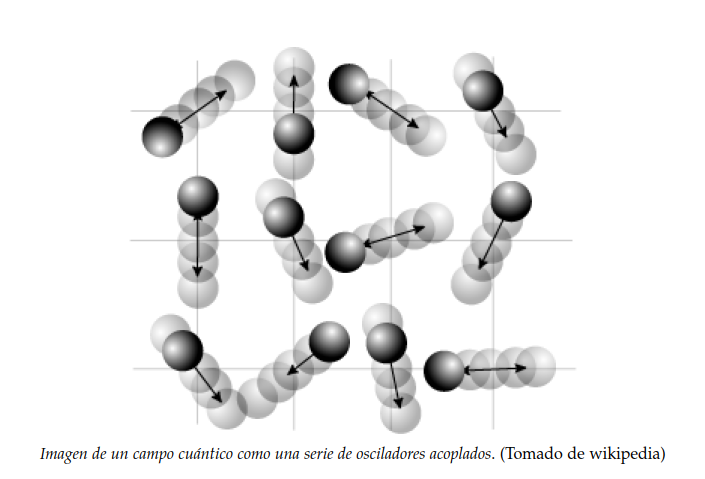
Ese último peldaño se ascendió con los primeros balbuceos de las teorías cuánticas de campos, las cuales concebían dichos campos de fuerzas como invisibles mallas de osciladores (algo similar a pequeñas masas unidas por muelles) extendidas por todo el espacio. Aplicando esta imagen al electromagnetismo, por ejemplo, las ondas electromagnéticas se explicarían como cambios en las tensiones de esos muelles que se propagan por el espacio obedeciendo una cierta ecuación diferencial (la ecuación de ondas). El hecho de que tales osciladores sólo puedan efectuar ciertos tipos de vibración, revela la vertiente cuántica de este fenómeno.
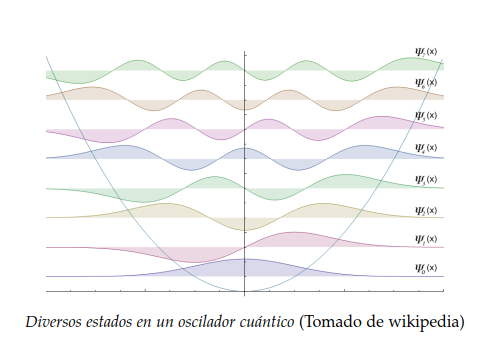
La táctica de razonar sobre los campos mediante modelos de osciladores cuantizados, contaba con una venerable tradición a sus espaldas. Basándose en trabajos previos de Max Planck (1900) sobre emisores oscilantes de energía, Otto Stern (1888 – 1969) y Albert Einstein (1879 – 1955) dedujeron en 1913 la existencia de una energía residual que todo oscilador cuántico debía poseer incluso aunque estuviese a la temperatura de cero grados Kelvin. Esa "energía del punto cero" (Nullpunktsenergie en alemán) era igual a la mitad del producto de la constante de Planck por la frecuencia mínima del oscilador. Como veremos más adelante, la constatación de que no parece haber una frecuencia mínima para muchos sistemas oscilatorios no hace más que oscurecer el problema.
Las célebres desigualdades de Heisenberg se utilizan a menudo para justificar esta energía remanente, dado que si uno de esos osciladores estuviese en perfecto reposo podrían determinarse a la vez con absoluta precisión su posición (en el punto de equilibrio) y su velocidad (igual a cero). Una situación tal se halla completamente prohibida por las desigualdades de Heisenberg, de modo que incluso en el cero absoluto el oscilador debe tener una distribución de valores de posición y de impulso (el producto de su masa por su velocidad) que satisfaga dichas desigualdades. Y ya que la energía es proporcional al impulso, ese mismo resultado implica que la energía del sistema también debe ser mayor que cero. En consecuencia, la física cuántica ni siquiera permite −como si hacía la clásica− un acercamiento arbitrario al cero absoluto, y por tanto tampoco al vacío absoluto.
Con un gran esfuerzo de la imaginación podemos admitir osciladores en los que siempre queda un residuo energético imposible de extraer, pero la situación empeora cuando nos referimos al espacio vacío. De acuerdo con la teoría cuántica, también allí hay algo. Entonces la mente se desboca, y suelen acudir las denominadas “relaciones de incertidumbre energía-tiempo”. En la mayoría de los manuales de divulgación al uso se cuenta que las desigualdades de Heisenberg se aplican también a la energía de un sistema y al tiempo que la posee (Desde luego que esto no es cierto. El tiempo, en palabras de Dirac, era una magnitud sin dispersión, y por ello no sometida a desigualdades como las de Heisenberg). Por este procedimiento, y como si fuese arte de magia, un objeto puede obtener energía de la nada a condición de que la devuelva en un tiempo tan breve que el universo no se dé por enterado.
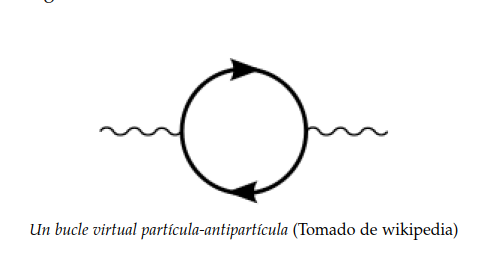
El vacío cuántico se comportaría, así pues, como un prestamista indulgente: nos permite desviarnos del equilibrio en nuestro balance energético, a condición de que tomemos menos cantidad de energía cuanto mayor sea el tiempo que dure el préstamo. Por eso, si tomamos prestada una gran cantidad de energía de la nada, tendremos que devolverla en un periodo proporcionalmente más breve; cuando somos menos codiciosos y la energía tomada es menor, su posesión puede durar algo más antes de devolverla a la nada de la que provino. Gracias a la equivalencia relativista entre masa y energía, estos préstamos energéticos se traducen en la aparición de partículas llamadas virtuales en el espacio vacío; partículas que acto seguido se aniquilan con una rapidez mayor cuanto más pesadas sean. La conservación de la energía se viola, es cierto, pero de una forma tan pudorosa que nadie puede dar testimonio de ello.
Naturalmente, eso no es lo que sucede, si bien la metáfora del préstamo cuya cuantía es inversamente proporcional a su duración, resulta muy fácil de manejar ante el público no experto. De hecho, la teoría cuántica sí respeta la conservación de la energía, y es curioso que la controversia que enfrentó a Einstein con Bohr sobre el llamado efecto BKS –en la que Bohr salió derrotado– giraba precisamente en torno a este tema. Se trataba de determinar si un cierto fenómeno atómico demostraba que la energía sólo se conservaba en sentido estadístico (es decir, como el promedio de muchos resultados) en algunos proceso cuánticos, o si probaba lo contrario. Los experimentos confirmaron la conservación estricta de la energía, y la postura de quienes opinaban como Einstein quedó reivindicada (Pais 1984, pp. 418 - 424).
1.5 Partículas virtuales
Al igual que cuando aplicamos razonamientos newtonianos a problemas relativistas –como si la relatividad fuese un simple retoque de la mecánica de Newton– solemos pensar sobre los problemas cuánticos en términos clásicos y nos vemos así enfrentados a paradojas insolubles. No es que la física cuántica sea diáfana en sus conceptos, pero sí tiene una lógica interna que, pese a desafiar nuestro sentido común, se respeta férreamente.
La metáfora que identifica las partículas virtuales con un crédito fugaz concedido por el vacío, parte de la idea del vacío clásico como algo ya establecido. Tenemos un vacío total perfectamente bien definido donde se respeta la conservación de la energía; y si aparecen de la nada parejas partícula-antipartícula, aunque luego se aniquilen, es porque dicha conservación se ha infringido. Pero no hay tal infracción, sino el fallo de olvidar que el vacío clásico –con sus características bien determinadas– simplemente no existe. Lo que realmente existe es ese vacío cuántico con una rica estructura, que de ningún modo debe considerarse como una alteración estrafalaria del vacío clásico.
En el vacío clásico –esa ficción inexistente en la realidad– para cualquier campo de fuerzas se anula tanto su valor medio como su desviación cuadrática media. Pensemos en un campo eléctrico ε para fijar ideas. La condición anterior significaría que hεi y hε2i son ambos iguales a cero. Por el contrario, en el vacío cuántico –el único realmente existente– se cumple hεi = 0, pero hε2i 6= 0. ¿Qué significa esto? Veamos un ejemplo sencillo para comprenderlo mejor.
Imaginemos dos corredores gemelos en el centro de un gimnasio que salen corriendo a la vez en sentidos opuestos hacia cada una de las paredes del recinto. Cuando llegan allí vuelven hacia su posición inicial la cruzan, llegan a la pared opuesta y comienzan el ciclo de nuevo. Suponiendo que parten en el mismo instante y corren siempre con igual velocidad, ambos atletas estarán en cada momento a la misma distancia del centro del gimnasio (nuestro origen de referencia) y sus velocidades tendrán signo contrario, de forma que el promedio será nulo. Pero si tomamos el cuadrado de dichas velocidades –lo que es una manera de prescindir del signo– observaremos que el promedio es distinto de cero.
Y ahí reside el nudo de la cuestión. La simetría del ejemplo impone que una magnitud estadística escogida para describir el sistema en su conjunto, el promedio de las velocidades de ambos corredores, se anule con respecto al origen de referencia escogido. Pero si prescindimos de los signos de las velocidades, indicativos de su orientación, y nos concentramos en otras características tales como el valor de la velocidad independiente del signo, comprobaremos que el promedio difiere de cero. Es obvio que si no hubiese corredores en absoluto ni el promedio ni la desviación cuadrática serían distintas de cero. Pues bien, trocando velocidades por intensidades de campo, el ejemplo de los corredores gemelos representaría el vacío cuántico y el caso de ausencia de corredores correspondería al vacío clásico.
¿Y no podríamos aislar una región del espacio eliminado de su interior todos los campos hasta llegar a una total ausencia de cualquier ente físico? La verdad es que no, porque ni siquiera en la física clásica –como ya vimos– es posible algo así. La física cuántica empeora la situación, dado que las partículas cuánticas se hallan deslocalizadas, y nunca podemos asegurar que no haya una cierta probabilidad de presencia suya en un lugar cualquiera.
Estas partículas cuánticas, o cuantones, también suelen hallarse en una combinación de estados de energía, que nos dará un valor promedio en torno al cual pueden darse desviaciones como sucede con cualquier magnitud estadística. Estas desviaciones serán tanto menos frecuentes cuanto más se aparten de la media. Y esa es la explicación que justifica el surgimiento de partículas virtuales en el vacío cuántico, no una fantasmagórica cesión de energía desde la nada. Además, incluso un vacío cuántico puede prepararse de diversos modos, lo que convierte en un asunto hasta cierto punto convencional la decisión de situar el cero de la escala de energías en un tipo de vacío o en otro. Contra la impresión que transmiten muchos textos divulgativos, también conserva su validez en la teoría cuántica el adagio filosófico de la antigua Grecia: “De la nada, nada sale”.
En términos de la teoría cuántica de campos, una región del espacio se considera en estado de vacío cuando en promedio se halla en su estado de menor energía. ¿Y cuál es esa energía mínima? Aquí llega otra de las claves de este problema, porque podríamos intentar calcularla simplemente sumando las energías residuales (“energías del punto cero”) de toda la red de osciladores que en nuestro modelo representan los diversos campos cuánticos. Pero como las frecuencias con menor longitud de onda –es decir, una frecuencia más alta– poseen mayor energía, si suponemos que el espacio es continuo, no hay límite a la pequeñez de las longitudes de onda posibles, y la suma de energías se hace infinita.
Una vía de escape consistiría en admitir que no sabemos si el espacio es realmente continuo, por lo cual sólo sumamos las energías remanentes de las vibraciones con una longitud de onda mayor que –por ejemplo– la longitud de Planck (unos 10–35 metros), lo que nos daría una densidad de energía finita pero enorme para el vacío; el equivalente a más de un kilogramo en cada centímetro cúbico. Sin embargo, a lo largo de todo este procedimiento estamos olvidando que el tratamiento de los campos cuánticos como redes de osciladores en vibración, únicamente sirve para campos libres, aquellos que no interactúan con ningún otro campo. Y no es ésa una suposición muy realista, en verdad.
Pese a todo, como la teoría cuántica de campos sólo se ocupa de variaciones de energía (la diferencia de un valor con respecto a otro cualquiera que tomamos de referencia), podemos añadir una constante arbitraria a la densidad de energía que hayamos definido sin alterar las predicciones teóricas sobre cualquier magnitud medible. Aprovechándonos no muy noblemente de esta ventaja, tenemos entera libertad para redefinir la densidad de energía del vacío restándole una cantidad constante igual a la energía del punto cero. Con ello conseguimos que la energía del vacío sea nula finalmente; un recurso generalmente bien acogido por los usuarios de la teoría cuántica de campos por cuanto parece librarles de un molesto estorbo (además, un estorbo infinito).
1.6 La radiación Hawking
Un caso especialmente flagrante se refiere a la explicación usualmente ofrecida sobre la radiación emitida por los agujeros negros, o “radiación Hawking” en homenaje a quien primero teorizó acerca de ella, el británico Stephen Hawking. Se acostumbra a comenzar diciendo que en el borde del horizonte de sucesos de un agujero negro, la indeterminación energía-tiempo permite la aparición de un par de partículas virtuales, Una de ellas –la antipartícula, por ejemplo– cae traspasando el horizonte de sucesos, región tras la cual resulta imposible escapar debido a la intensísima atracción gravitatoria que retiene incluso la luz. Privada de su compañera la otra componente de la pareja no tiene ya con qué aniquilarse de modo que puede escapar convertida ahora en una partícula real.
¿Qué ocurre aquí con ese velo de fugacidad que ocultaba tan descarado incumplimiento de la conservación de la energía? A esto se replica indicando que la antipartícula engullida portaba una cantidad de energía “negativa” que compensaba la energía positiva de su compañera liberada, pero al caer tras el horizonte de sucesos esa energía negativa ha cancelado parte de la energía positiva poseída por el agujero negro reduciendo su tamaño. Desde fuera, no obstante, todo se contempla como una emisión de partículas por parte del agujero negro –la radiación Hawking– que se encoge y además ya no es tan negro. Dejemos hablar al propio Hawking (1988):
«(. . . ). Como la energía no puede ser creada de la nada, uno de los componentes de un par partícula/antipartícula tendrá energía positiva y el otro energía negativa. El que tiene energía negativa está condenado a ser una partícula virtual de vida muy corta, porque las partículas reales siempre tienen energía positiva en situaciones normales. Debe, por lo tanto, buscar a su pareja y aniquilarse con ella. Pero una partícula real, cerca de un cuerpo masivo, tiene menos energía que si estuviera lejos, porque se necesitaría energía para alejarla en contra de la atracción gravitatoria de ese cuerpo.
Normalmente, la energía de la partícula aún sigue siendo positiva, pero el campo gravitatorio dentro de un agujero negro es tan intenso que incluso una partícula real puede tener allí energía negativa. Es, por lo tanto, posible, para la partícula virtual con energía negativa, si está presente un agujero negro, caer en el agujero negro y convertirse en una partícula o antipartícula real. En este caso, ya no tiene que aniquilarse con su pareja. Su desamparado compañero puede caer así mismo en el agujero negro. O, al tener energía positiva, también puede escaparse de las cercanías del agujero negro como una partícula o antipartícula real (. . . ). Para un observador lejano, parecerá haber sido emitida desde el agujero negro. Cuanto más pequeño sea el agujero negro, menor será la distancia que la partícula con energía negativa tendrá que recorrer antes de convertirse en una partícula real y, por consiguiente, mayores serán la velocidad de emisión y la temperatura aparente del agujero negro.
La energía positiva de la radiación emitida sería compensada por un flujo hacia el agujero negro de partículas con energía negativa. Por la ecuación de Einstein E=mc2 (en donde E es la energía, m, la masa y c, la velocidad de la luz), sabemos que la energía es proporcional a la masa. Un flujo de energía negativa hacia el agujero negro reduce, por lo tanto, su masa. (. . . )»
Tan rocambolesca explicación se simplificaría mucho si nos limitásemos a señalar lo que verdaderamente ocurre, a saber, que parte de la energía del campo gravitatorio del agujero negro se manifiesta como pares partículaantipartícula, una de las cuales tiene cierta probabilidad de escapar del horizonte de sucesos por la deslocalización de sus posiciones espaciales. El balance final es que el agujero negro, en efecto, ha perdido parte de su energía y se ha contraído levemente, sin necesidad de apelar a estrambóticas energías “negativas”.
No sólo es que la teoría cuántica respeta la conservación de la energía, sino que tampoco necesitamos en modo alguno recurrir a energías negativas –el potencial gravitatorio newtoniano tiene un signo negativo convencional, tan solo para denotar el carácter esencialmente atractivo de la gravitación– de difícil interpretación física. Porque debido a la equivalencia masa-energía relativista, una energía negativa implicaría la presencia de masas negativas con inercias negativas (Terletski 1968, pp. 83 – 116) y, a causa del principio de Equivalencia de Einstein, también gravitaciones negativas. Un precio demasiado elevado a pagar en la coherencia de nuestra imagen de la naturaleza, a cambio de una muy discutible sencillez en la divulgación de un fenómeno físico sin duda fascinante como la radiación de los agujeros negros.
Tampoco debemos olvidar que los estados de energía negativa surgen en el escarpado terreno del método de perturbaciones, una técnica de cómputo diseñada para calcular mediante aproximaciones sucesivas el resultado de ciertos procesos cuánticos donde sólo los estados inicial y final poseen un inequívoco sentido físico. Los estados intermedios carecen de semejante garantía, y de ahí el adjetivo “virtuales” que los acompaña. Curiosamente, los autores que repiten el relato de la incertidumbre energía-tiempo, violando transitoriamente la conservación de la energía, nunca sugieren que se infrinja la conservación de la carga eléctrica; los cuantones virtuales siempre aparecen como pares partícula-antipartícula. Y sin embargo, las mismas razones –ninguna, de hecho– habría para incumplir ambos teoremas de conservación.
1.7 Nuestro amigo el bosón de Higgs
Los comentarios precedentes podrían haber bastado con anterioridad a 1964, pues fue en ese año cuando diversos autores, entre los cuales el más célebre es Peter Higgs, propusieron la existencia de una nueva partícula que se conocería en adelante como el bosón de Higgs. Se trataba de encontrar un camino hacia la unificación del electromagnetismo y la fuerza nuclear débil, para lo cual era necesario explicar la gran disparidad existente entre la masa del fotón, cuanto asociado al campo electromagnético, y los bosones W+, W− y Z0, propios de la fuerza nuclear débil. Higgs y sus colegas propusieron la existencia de una nueva partícula, un nuevo campo cuántico universal extendido por todo el espacio, que al interactuar con las partículas conocidas explicaría los valores de sus masas, bien medidos experimentalmente pero sin justificación teórica.
De ahí nació la metáfora del sombrero mejicano, donde los sistemas físicos han de optar entre una situación de elevada simetría energéticamente inestable, y otra con menos energía, mayor estabilidad y menos simetría. La situación altamente simétrica representaba el caso en el que la fuerza nuclear débil y el electromagnetismo se hallaban unificados (todos los bosones carecían de masa, como el fotón), mientras que la pérdida de simetría indicaba la ruptura de dicha unificación para llegar al estado actual.
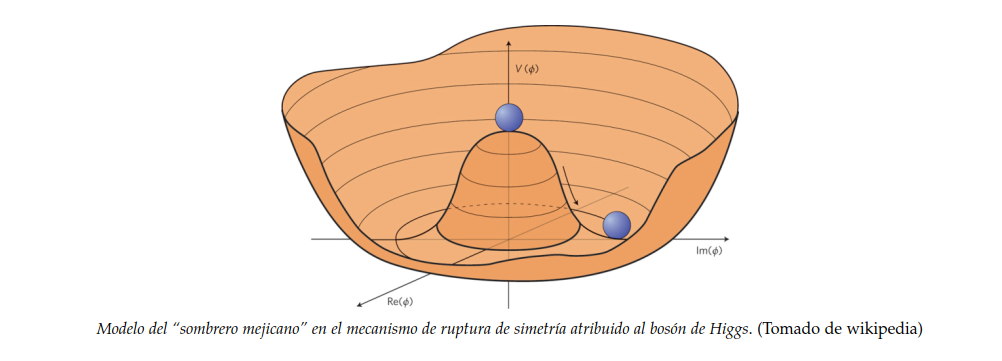
Resultaba, pues, que además del esquema de osciladores invisibles impuesto en todas partes por la teoría cuántica de campos como modelo para el vacío cuántico, ahora teníamos un campo adicional que llenaba todo el espacio como el desaparecido éter del siglo XIX. Era una razón más para no considerar "vacío" el vacío, en especial porque a diferencia de los campos cuánticos usuales el campo de Higgs posee un valor medio distinto de cero en el vacío, en todo lugar y en todo instante. Esto no es un efecto residual o remanente, achacable a la dispersión de ciertas magnitudes físicas sometidas a las desigualdades de Heisenberg. El campo de Higgs aspira a ser considerado una pieza omnipresente en la arquitectura básica del cosmos, sin la cual el resto de partículas elementales no podría dar cuenta del valor que tienen sus masas.
No es de extrañar que la búsqueda de este singular bosón se haya convertido en uno de los principales objetivos de la física experimental de altas energías a comienzos del siglo XX. Lo cierto es que el 4 de julio de 2012, el equipo de investigación del Gran Colisionador de Hadrones, dependiente del CERN en Ginebra, anunció con solemnidad que los datos recogidos hasta ese momento avalaban la existencia de un cuantón como el conjeturado por Higgs. Sin duda fue un momento histórico en la física experimental, como siempre que se descubre una nueva partícula; otra cosa es que este cuantón desempeñe el papel que Higgs y sus colegas le atribuyen.
¿Qué dificultades hay con el bosón de Higgs? Si lo pensamos bien, el modelo del sombrero mejicano es tan solo lo que los anglosajones llaman a just-so story, un relato de algo que simplemente “es así”. Nos parece convincente porque en la vida real, debido a la gravedad y a las ecuaciones dinámicas de Newton, todos sabemos que una bolita sobre la copa de un sombrero mejicano caerá sobre el ala más pronto que tarde. Sin embargo, en el mundo ultramicroscópico no hay una contrapartida a la gravedad o a las ecuaciones de Newton que gobiernen la transición desde el estado inicial al final. Meramente se nos dice que ocurre así, y probablemente sea cierto, pero seguimos sin saber por qué.
Este hecho ha propiciado que los físicos se distribuyan en tres escuelas, la primera de las cuales confía en que el bosón de Higgs sea descubierto y posea las propiedades que se le suponen sin mayores controversias. Y así parece que ha ocurrido. La segunda línea de pensamiento apostaba por la inexistencia del bosón de Higgs, y especulaba con la posibilidad de nuevos mecanismos de ruptura de simetría que permitan avanzar hacia una nueva física no contemplada por el Modelo Standard de la física de partículas. Sin embargo, el anuncio del 4 de julio de 2012 en el CERN ha desmentido casi por completo esta posibilidad. Por último, el tercer grupo acepta que el bosón de Higgs existe, aunque seguramente no cumplirá las funciones que de él se espera, lo que nos obligaría a replantear el mecanismo de ruptura de simetría que subyace en la teoría de unificación electrodébil. Sólo el tiempo decidirá quién tiene razón, si es que alguien la tiene y no acaba aflorando otra opción distinta de todas estas.
Otro interrogante surge cuando tratamos de explicar cómo logró la simetría electrodébil romperse de manera idéntica en todos los puntos del universo. Es decir, ¿por qué los fotones que recibimos desde la galaxia de Andrómeda tienen exactamente las mismas propiedades que los procedentes de nuestro Sol? En principio no tendría por qué ser así, pero de hecho así es, y la familiaridad con este dato ha oscurecido con frecuencia el misterio de su origen. Ahora bien, quizás el aspecto más inquietante del bosón de Higgs es que pretende explicar el valor de las masas de las partículas elementales, y las masas constituyen la fuente de la gravedad. La gravitación ha sido hasta el momento la gran ausente de este debate; hora es ya que dejemos paso a la más venerable y omnipresente de las fuerzas.
1.8 El problema de la gravedad
La gravitación, introducida en la visión científica del mundo mediante la ley newtoniana de atracción universal, se contempla hoy día a través de los ojos de Einstein como un efecto de la curvatura del espacio-tiempo (Misner et al. 1973, Gray 1992). Si nos imaginamos ese entramado de espacio y tiempo que en relatividad se denomina “espacio-tiempo”, como si fuese una lámina elástica sobre cuya superficie descansan todas las masas del universo, la curvatura producida por dichas masas sería el fenómeno físico que históricamente decidimos llamar “gravedad”. Pero esa costumbre no tenía más motivos que la falta de la adecuada perspectiva en cuatro dimensiones que nos vino a ofrecer el espacio-tiempo de la relatividad general, la teoría de Einstein para la gravedad.
Las órbitas de los planetas en torno al Sol, que antes creíamos líneas rectas desviadas por la atracción de la gravedad, ahora resultan ser las trayectorias menos torcidas –las “geodésicas”– sobre un fondo espacio-temporal curvado. Y esa es la raíz del obstáculo que ahora encontramos. Si la fuerza gravitatoria desaparece en la imagen relativista sustituida por la geometría espacio-temporal, el concepto de energía gravitatoria también pierde su significado ordinario. La energía es una magnitud que se aplica a los campos de fuerzas, y si tales campos quedan reemplazados por otro concepto, la energía a ellos asociada deja de tener sentido (Kragh 1996). Por eso no es del todo correcto identificar la constante cosmológica, como se hace usualmente, con la densidad de energía del vacío cuántico.
La constante cosmológica es un término de las ecuaciones de la relatividad general referido a la curvatura intrínseca del espacio-tiempo, en ausencia de la materia y la radiación que llenan el universo. Aun cuando desempeñe un papel comparable al de la densidad energética del vacío en la teoría cuántica, su origen conceptual es radicalmente distinto (Padmanabhan 2003, Nobbenhuis 2006), y sólo por un abuso de lenguaje equiparamos ambas magnitudes. No obstante podemos entrar en ese juego y ver hasta dónde nos lleva.
Interpretando la constante cosmológica en términos de una densidad energética del vacío (Birrel y Davies 1982), las observaciones astronómicas nos dicen que debe ser muy cercana a cero (unos 10–29 gramos/cm3) y positiva, ya que el universo parece acelerar su expansión (Kowalski et al. 2008). Ciertamente, para llegar a esas conclusiones, además de los datos empíricos, necesitamos aceptar ciertas hipótesis cosmológicas muy generales y confiar en la pertinencia de la relatividad general. Sea como fuere, el hecho fundamental es que la densidad energética del vacío deducida empleando la gravedad de Einstein, ha de ser muy próxima a cero, pues de lo contrario debería haber algo profundamente equivocado en la relatividad general, una teoría que nos ha venido proporcionando algunas de las mejores verificaciones experimentales de la historia de la física.
El cálculo de la densidad de energía del vacío a través de la teoría cuántica de campos, como vimos en un apartado anterior, puede arrojar un resultado nulo, infinito o finito pero inmensamente grande, según las premisas de nuestro razonamiento. Pero la relatividad general suele recordarnos que en todos estos casos estamos olvidando el papel de la gravedad. Es por ello que en muchas ocasiones se prefiere afirmar meramente que la densidad de energía del vacío no está definida, pues una misma teoría nos ofrece tres resultados posibles, y aun eso omitiendo la influencia de la interacción que posiblemente sea la más importante, la gravedad.
1.9 Conclusiones
Desde el comienzo de su investigación científica, el vacío –y en concreto el vacío cuántico– se nos ha revelado como un tema de investigación asombroso y prometedor. Lejos de la idea popular de una especie de “nada” carente de todo interés, la riqueza de sus estructuras, la distancia que separa sus propiedades de nuestras intuiciones ordinarias y la complejidad de los fenómenos que lo caracterizan, seguirán dando material de trabajo a los investigadores durante mucho tiempo.
No obstante, ya sabemos que para explorar sus misterios, igual que para explicarlos con un nivel divulgativo, sobran las tergiversaciones conceptuales, como aquellas que se basan en una supuesta violación de la ley de conservación de la energía. Y tampoco necesitamos recurrir a conceptos sin encaje en otras ramas de la física, como las energías “negativas”, rebosantes de connotaciones nada científicas.
La búsqueda del vacío perfecto se ha aferrado a la historia humana no con tanta popularidad pero sí con la misma intensidad que muchos otros ideales quiméricos, ya concerniesen al elixir de la eterna juventud, o a la piedra filosofal que todo lo convertía en oro. Al final, el vacío absoluto se difuminó junto con la velocidad infinita o el movimiento continuo en el viejo baúl de imposibilidades físicas que durante mucho tiempo desvelaron los sueños de los intelectos más inquietos. Para sustituirlo llegó un reemplazo no menos fascinante, el vacío cuántico, con un cortejo de paradojas, confusiones y nuevas utopías científicas. Tantas y tan bien justificadas perplejidades tenían su origen en el peculiar comportamiento de los sistemas cuánticos, lo que nos brindó una nueva oportunidad de poner a prueba la solidez de los prejuicios cotidianos que llamamos “sentido común”.
Gracias a este nuevo reto sabemos que para llegar a buen puerto en cualquier excursión al mundo cuántico, basta con pertrecharnos de una buena dosis de respeto por los datos experimentales, coherencia en nuestros argumentos y una consideración cuidadosa de los conceptos empleados. Aun así no es poco, pero sin duda la recompensa vale la pena.
Bibliografía
-
Aitchison, I.J.R. (1985) "Nothing’s plenty. The vacuum in modern quantum field theory", Contemporary Physics 26: 333-391.
-
Birrell, N.D., Davies, P.C.W. (1982). Quantum Fields in Curved Space. Cambridge University Press: Cambrdige(U.K.).
-
De Segovia, J.L. (2010). "Historia del vacío desde Grecia a finales del siglo XIX", Revista Española de Física 24 (2): 58-66.
-
Einstein, A., Stern, O. (1913). "Einige Argumente für die Annahme einer molekularen Agitation beim absoluten Nullpunkt". Annalen der Physik 40 (3): 551.
-
Gaukroger, S. (2002). Descartes’ System of Natural Philosophy. Cambridge University Press: Cambridge (U.K.).
-
Gray, J. (1992). Ideas de Espacio. Mondadori: Madrid
-
Hawking, S. (1988). Historia del Tiempo, Crítica: Barcelona.
-
Kowalski, M. et al. (2008). "Improved Cosmological Constraints from New, Old and Combined Supernova Datasets", Astrophysical Journal 686: 749-778.
-
Kragh, H. (1996). Cosmology and Controversy. Princeton University Press: Princeton.
-
Lorentz, H.A. (1927). Aether theories and aether models (Lectures on Theoretical Physics vol. I). MacMillan and Co. Ltd: London.
-
Maxwell, J.C. (1873). A Treatise on Electricity and Magnetism. Clarendon Press: Oxford.
-
Maxwell, J.C. (1890). The Scientific Papers of James Clerk Maxwell (W.D. Niven, ed.). Cambridge University Press: Cambridge (U.K.).
-
Misner, C., Thorne, K., WheeleR, J.A. (1973). Gravitation. Freeman: New York. Nobbenhuis, S. (2006). "Categorizing Different Approaches to the Cosmological Constant Problem", Foundations of Physics 36: 613-680.
-
Padmanabhan, T. (2003). "Cosmological constant – the weight of the vacuum", Physics Reports 380: 235–320. Pais, A. (1984). El Señor es sutil... La ciencia y la vida de Albert Einstein, Ariel (Barcelona), 1984.
-
Planck, M (1900). "Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum". Verhandlungen der Deutschen Physikalischen Gesellschaft 2: 237–245.
-
Rugh, S. E.; Zinkernagel, H. (2002). "The Quantum Vacuum and the Cosmological Constant Problem". Studies in History and Philosophy of Modern Physics, vol. 33 (4): 663–705.
-
Terletski, Y.P. (1968). Paradoxes in the Theory of Relativity, Plenum Press: New York.
-
Wikipedia. Imágenes de libre uso tomadas de la Enciclopedia Virtual.
Vídeo

































